Cách xét tính đơn điệu của hàm số y=f(u) dựa vào đồ thị hàm số y=f'(x) được soạn dưới dạng file word và PDF gồm 6 trang. Các bạn xem và tải về ở dưới.
I. Phương pháp
+ Từ đồ thị của hàm số $y = f'(x)$, suy ra dấu của $f'(x)$.
+ Tính $g'(x)$ và lập bảng biến thiên của hàm số $y = g(x)$, suy ra dấu của $g'(x)$.
+ Kết luận về tính đơn điệu của hàm số $y = g(x)$.
Chú ý:
-Trên khoảng $\left( {a;b} \right)$, đồ thị của hàm số $y = f'(x)$ nằm phía trên trục hoành thì $f'(x) > 0,\,\forall x \in \left( {a;b} \right)$.
-Trên khoảng $\left( {a;b} \right)$, đồ thị của hàm số $y = f'(x)$ nằm phía dưới trục hoành thì $f'(x)
– Đồ thị của hàm số $y = f'(x)$ cắt trục hoành tại điểm ${x_0}$ thì $f'({x_0}) = 0$.
II. Các ví dụ
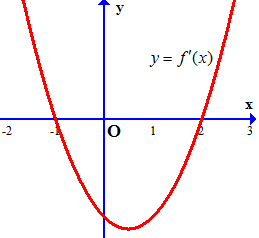
Ví dụ 1. Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đồ thị đạo hàm $f’\left( x \right)$ là hàm số bậc hai như hình vẽ.
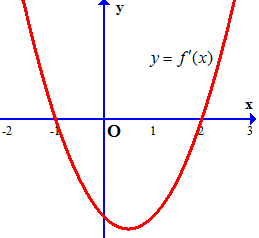
Tìm các khoảng đồng biến, nghịch biến của hàm số $y = g(x) = f\left( {7 – 2x} \right)$.
Lời giải
Chú ý: $y = f(u) \Rightarrow y’ = {\left[ {f(u)} \right]^\prime } = u’f'(u)$
Ta có:
$g'(x) = {\left[ {f\left( {7 – 2x} \right)} \right]^\prime }$$ = {\left( {7 – 2x} \right)^\prime }f’\left( {7 – 2x} \right) = – 2f’\left( {7 – 2x} \right)$
$g'(x) = – 2f’\left( {7 – 2x} \right) = 0$$ \Leftrightarrow f’\left( {7 – 2x} \right) = 0$
$ \Leftrightarrow \left[ \begin{gathered}
7 – 2x = – 1 \hfill \\
7 – 2x = 2 \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
x = 4 \hfill \\
x = \frac{5}{2} \hfill \\
\end{gathered} \right.$.
Bảng biến thiên của hàm số $y = g(x)$
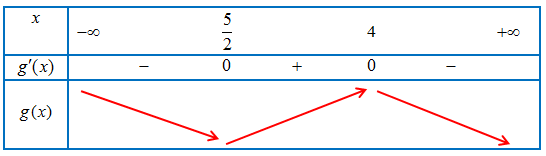
Vậy hàm số $y = g(x)$
– Đồng biến trên khoảng $\left( {\frac{5}{2};4} \right)$.
– Nghịch biến trên các khoảng $\left( { – \infty ;\frac{5}{2}} \right)$ và $\left( {4; + \infty } \right)$.
Ví dụ 2. Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đồ thị đạo hàm $f’\left( x \right)$ là hàm số bậc ba như hình vẽ.
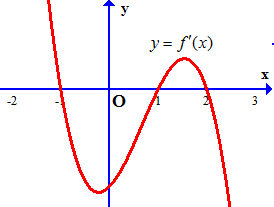
Tìm các khoảng đồng biến, nghịch biến của hàm số $y = g(x) = f\left( {{x^2}} \right)$.
Lời giải
Ta có:
$g'(x) = {\left[ {f\left( {{x^2}} \right)} \right]^\prime }$$ = {\left( {{x^2}} \right)^\prime }f’\left( {{x^2}} \right) = 2xf’\left( {{x^2}} \right)$
$g'(x) = 2xf’\left( {{x^2}} \right) = 0 \Leftrightarrow \left[ \begin{gathered}
2x = 0 \hfill \\
f’\left( {{x^2}} \right) = 0 \hfill \\
\end{gathered} \right.$
$ \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
{x^2} = – 1\,\,(vô\,nghiệm) \hfill \\
{x^2} = 1 \hfill \\
{x^2} = 2 \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
x = \pm 1 \hfill \\
x = \pm \sqrt 2 \hfill \\
\end{gathered} \right.$
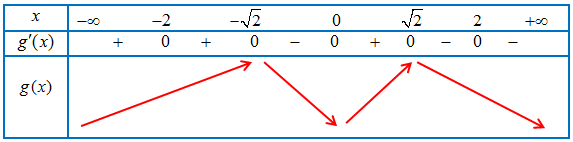
Bảng biến thiên của hàm số $y = g(x)$
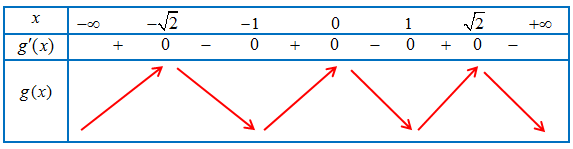
Vậy hàm số $y = g(x)$
– Đồng biến trên các khoảng $\left( { – \infty ; – \sqrt 2 } \right)$, $\left( { – 1;0} \right)$ và $\left( {1;\sqrt 2 } \right)$.
– Nghịch biến trên các khoảng $\left( { – \sqrt 2 ; – 1} \right)$, $\left( {0;1} \right)$ và $\left( {\sqrt 2 ; + \infty } \right)$.
Ví dụ 3. Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đồ thị đạo hàm $f’\left( x \right)$ là hàm số bậc ba như hình vẽ.
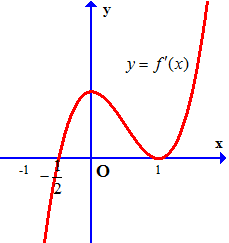
Tìm các khoảng đồng biến, nghịch biến của hàm số $y = g(x) = f\left( {\frac{1}{4}{x^2} – \frac{1}{4}} \right)$.
Lời giải
Ta có:
$g'(x) = {\left[ {f\left( {\frac{1}{4}{x^2} – \frac{1}{4}} \right)} \right]^\prime }$$ = {\left( {\frac{1}{4}{x^2} – \frac{1}{4}} \right)^\prime }f’\left( {\frac{1}{4}{x^2} – \frac{1}{4}} \right)$ $ = \frac{1}{2}xf’\left( {\frac{1}{4}{x^2} – \frac{1}{4}} \right)$
$g'(x) = \frac{1}{2}xf’\left( {\frac{1}{4}{x^2} – \frac{1}{4}} \right) = 0 \Leftrightarrow \left[ \begin{gathered}
\frac{1}{2}x = 0 \hfill \\
f’\left( {\frac{1}{4}{x^2} – \frac{1}{4}} \right) = 0 \hfill \\
\end{gathered} \right.$
$ \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
\frac{1}{4}{x^2} – \frac{1}{4} = – \frac{1}{2} \hfill \\
\frac{1}{4}{x^2} – \frac{1}{4} = 1 \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
{x^2} = – 1\,(vô\,nghiệm) \hfill \\
{x^2} = 3 \hfill \\
\end{gathered} \right.$
$ \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
x = \pm \sqrt 3 \hfill \\
\end{gathered} \right.$
Bảng biến thiên của hàm số $y = g(x)$
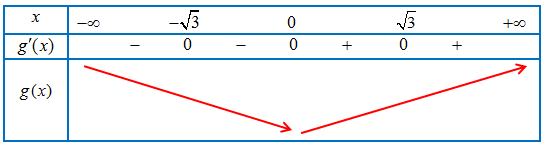
Vậy hàm số $y = g(x)$
– Đồng biến trên khoảng $\left( {0; + \infty } \right)$.
– Nghịch biến trên khoảng $\left( { – \infty ;0} \right)$.
Ví dụ 4. Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đồ thị đạo hàm $y = f’\left( x \right)$ hình vẽ.
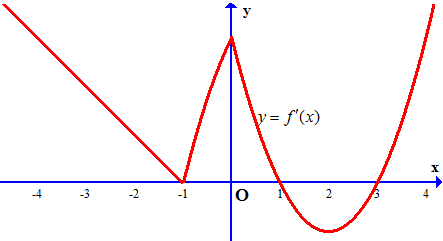
Tìm các khoảng đồng biến, nghịch biến của hàm số $y = g(x) = f\left( { – {x^2} + 3} \right)$.
Lời giải
Ta có:
$g'(x) = {\left[ {f\left( { – {x^2} + 3} \right)} \right]^\prime }$$ = {\left( { – {x^2} + 3} \right)^\prime }f’\left( { – {x^2} + 3} \right) = – 2xf’\left( { – {x^2} + 3} \right)$
$g'(x) = – 2xf’\left( { – {x^2} + 3} \right) = 0 \Leftrightarrow \left[ \begin{gathered}
– 2x = 0 \hfill \\
f’\left( { – {x^2} + 3} \right) = 0 \hfill \\
\end{gathered} \right.$
$ \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
– {x^2} + 3 = – 1 \hfill \\
– {x^2} + 3 = 1 \hfill \\
– {x^2} + 3 = 3 \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
{x^2} = 4 \hfill \\
{x^2} = 2 \hfill \\
{x^2} = 0 \hfill \\
\end{gathered} \right.$ $ \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
x = \pm 2 \hfill \\
x = \pm \sqrt 2 \hfill \\
x = 0 \hfill \\
\end{gathered} \right.$
Bảng biến thiên của hàm số $y = g(x)$
Vậy hàm số $y = g(x)$
– Đồng biến trên các khoảng $\left( { – \infty ; – \sqrt 2 } \right)$ và $\left( {0;\sqrt 2 } \right)$.
– Nghịch biến trên các khoảng $\left( { – \sqrt 2 ;0} \right)$ và $\left( {\sqrt 2 ; + \infty } \right)$.
———-